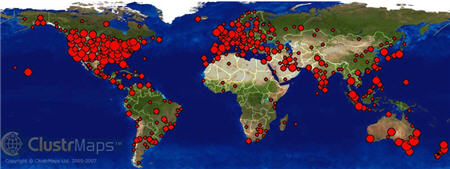
Have you looked at your ClustrMaps recently?
Are you like me? Do the growing red dots make you want to learn more about all your visitors, their lives, where they live and amaze you with how the Internet has brought us all together?
Pleased to hear because you’ve all got me into trouble! Students are checking closely The Edublogger ClustrMaps as well as their own!
They all want more dots on their ClustrMaps!
Can you leave a comment (or write a post) to share your tips and advice on any (or all) of the following:
- What are 3 ways for students to increase their blog readership (while also increasing their learning through blogging)?
- What advice would you give students about writing comments on other people’s blogs?
- What are some of the aspects of blog etiquette that students need to consider when trying to increase their readership?
HELP: If you are from Madagascar, or know someone who lives in Madagascar, can you please visit (or get them to visit) Sahana’s post and leave a comment! Read her comment here (as svbsky) to understand why I’m asking 😎
FINAL THOUGHTS
ClustrMaps is a “must-have” widget for class and student blogs because it reminds students that they are part of a global audience.
Here are the instructions for adding a ClustrMaps to your blog sidebar using:
- The ClustrMaps Widget – Edublogs supporters only
- A Text Widget – free Edublogs users
If you are enjoying reading this blog, please consider ![]() Subscribing For Free!
Subscribing For Free!
hi Sue Waters!!!
just like the Madagascar problem i have another one for you. I need someone from the Bahams. My friend that i told you about, is going to the Bahamas, and she doesn’t know if her laptop is going to work so i’m asking you. Thanks a bunch!!!!!
-Sahana
Hi Sahana, in this case she probably needs to contact the hotel where she is staying because each situation is different.
Many of my students are still struggling with the concept, but here is a great example:
Victoria read SamH’s post about heros (http://samh16.edublogs.org/2009/05/04/heros/) and asked herself “Do I agree with any of Sam’s choices? Why or why not?”
Her comment:
“Hi, I agree with you, Ghandi was a great inspiration for me too, I thought i was the only one that understood Ghandi he was strong with words,he fought with words and no matter how much he tried he NEVER gave up he is truly one of my HEROS.”
Punctuation and grammar aside, what author wouldn’t love to get a response that actually pertains to their post?
I created a “cheat sheet” of higher order thinking questions and prompts adapted from several teaching websites, trainings and conversations with other teachers that are used throughout our curriculum. The students “self-interview” and apply the questions to the post they are reading until one is a good fit.
For example:
– Give an example of POST TOPIC (PT) in your own life.
– What is the relationship of PT to something you know about?
– How is PT like or dislike something in our classroom or at your home?
– Based on what you read what can you conclude about PT?
– What was the authors point or opinion? Do you agree or disagree with it and why?
We started by reading other blogs as a class and had whole class discussions about the posts before students were asked to comment on specific posts. My plan is to start at the beginning of our school year next August (as opposed to March!) and really incorporate reading and responding early on.
Thanks for sharing your examples of how you are approaching it with your students. It is a really hard task. Adults also struggle with this aspect.
I’m slowly convincing Sue Wyatt about the idea of a comment challenge for August/September — but we will need to wait and see.
They have a version of this on facebook where you dot the cities / countries you’ve visited (eg Thailand, Indonesia etc).
Okay Kratom, I confess to being a neglectful Facebook but make up for it with my twitter addiction. So can you tell me which application in Facebook 🙂
Off course mine wouldn’t have many dots 🙁
I try to encourage my students to think as themselves as the author and create a question they could include in their post (as I do to encourage commenting). When they have thought of the question, they comment with the answer. I have seen some very creative and insightful commenting from students using the “self interview” method.
Thanks that sounds like a really excellent method. Have you written it up any where? Also can you give me some likes to excellent examples of where students have done this well because getting them to write meaningful comments can be challenging.
It would be great to have some links good commenting practice by students.
Hi Sue,
I’m pasting below a comment I wrote about Clustrmaps while back in celebration of the Edublogger’s first birthday:
Favorite Blog Widget: ClustrMaps – Last year I was helping Jim Faires, a 6th grade teacher in my district, get his students up and running with YouthRadio, a collaborative project developed by Kevin Hodgson. Jim was introducing his students to podcasting. The question he posed to the class was “What if the whole world was your audience?!”
When the students completed their podcast, they watched as Jim uploaded it to the YouthRadio blog. It was then that one of the them spotted the ClustrMap. Jim opened the enlarged view. Try to imagine their amazement and exuberance when they realized the blog had visitors from all parts of the world and every continent (ok, not Antarctica). Suddenly students were scurrying for an atlas to accurately identify each state and country.
Not only was the ClustrMap a built-in geography lesson, but it also illustrated and answered Jim’s question: truly, the whole world had become their audience.
Thanks Gail for adding what you wrote about Clustrmaps to celebrate the Edublogger’s first birthday. Tools like ClustrMaps immediately show that global audience.
I’ve seen educators make ClustrMaps cakes to celebrate. I’m also sure I’ve seen them post World maps on their wall and get their students to add information. But I can’t remember where? Have you seen any links that shows physical maps used this way with ClustrMaps or a Google Map?
Kia ora Sue!
The Comment Challenge May 2008 taught me a lot about 1, 2 and 3.
Here’s a summary of what I found has been useful over a year’s blogging and that I learnt during the 31 Day Comment Challenge:
1
(a) keep learning and improving post writing technique by posting regularly
(b) read other bog posts regularly and comment on them where and when appropriate
(c) give of yourself when you post and/or comment – include useful links to relevant resources, and useful sites especially other blog posts
2
When writing on other blog posts do a bit of thinking first (see Homer’s Comment 8 tips) think about what you are going to write in your comment and if possible draft it in notepad first and keep it friendly.
3
Keep it friendly. Responding using the name of the person who is posting (or who is commenting) helps with this (see U Comment 5 ways).
Catchya later
from Middle-earth
Hi Ken, I’m glad you highlighted the comment challenge and how much you gained from it. Thanks for sharing some of what you learnt.
Bonnie has asked me if we are going to run it again and I’m definitely thinking about it. I see blogging as something that can be broken into the two components; those that improve blogging and design skills; and those that look at the commenting aspect.
Trouble is I have all these projects I want to do but time is the challenge 🙁
Howja eat an elephant?
The 3 easiest ways to increase your blog readership (while increasing your learning through blogging) are:
Blog about interesting things – things that you are passionate about or feel strongly about – if you’re interested in them, chances are someone else out there is too!
Tag and categorise properly. This makes it so much easier to for people to find the things that you are talking about.
Go read and comment on other people’s blogs. And always fill out the link website space with your blog’s URL so that the blogger can check your blog out too! If there’s no link space to fill out – hyperlink your blog at the end of your comment.
Which leds me to Question 2 quite nicely. Don’t just comment things like – “wow, that’s so cool” or “I like your blog” (we call those ‘weasel word’ comments). Actually respond to the blog post – agree, disagree, explain your point of view, say what you are thinking and why you are thinking that. But always be polite! (And that answers Question 3 at the same time!!)
Hi Chrissy, tags and categories are interesting and as you say really important.
However educators themselves struggle with using them effectively which is probably why I see students not using them. What advice would you give teachers on teaching their students how to use?
Good commenting practice, as opposed to “wow, that’s so cool” and now “visit my blog”, has been a challenge during the Student blogging challenge. Personally I think because that is when you are taking the students to the next level and it does take time. What do you think? How do you try to encourage/ensure your students are commenting well?
I have gone a step further and got a live Clustr map as well with
http://whos.amung.us/
If more than one person is looking at your blog in real time you get more pulsing dots to show that they are live. Kids get a real kick out of seeing multiple pulsing dots from different parts of the globe.
Have a look down the bottom right hand side of my class blog for a working example.
http://moturoa.blogspot.com/
Yes Allanah, that is way cool! Could imagine sending out a twitter and getting the map light up in front of their eyes.